Ekuivalensi Antar Deterministic Finite Automata (DFA)
Ekuivalensi Antar Deterministic Finite Automata (DFA)
Tujuan kita adalah mengurangi jumlah state dari suatu finite state automata, dengan tidak mengurangi kamampuannya semula untuk menerima suatu bahasa.
Ada 2 istilah yang perlu kita ketahui yaitu :
- Distinguishable : dapat dibedakan
- Indistinguishable : tidak dapat dibedakan
Reduksi Jumlah State Pada FSA
Reduksi dilakukan untuk mengurangi jumlah state tanpa mengurangi kemampuan untuk menerima suatu bahasa seperti semula (efisiensi). State pada FSA dapat direduksi apabila terdapat useless state. Useless State yaitu bukan state awal, tidak menerima nilai input dari state lain tetapi memberikan nilai input ke state lain. Hasil dari FSA yang direduksi merupakan ekuivalensi dari FSA semula.
Pasangan State dapat dikelompokkan berdasarkan :
- Distinguishable State (dapat dibedakan)
- Indistingushbale (tidak dapat dibedakan)
Reduksi Jumlah State Pada FSA - Relasi
Pasangan dua buah state memiliki satu kemungkinan : Distinguishable atau Indistingushbale. Tetapi tidak kedua-duanya. Dalam hal ini terdapat sebuah relasi :
Jika p dan q adalah Indistingushbale,
dan q dan r adalah Indistingushbale
maka p, r adalah Indistingushbale dan
p, q, r adalah Indistingushbale
Dalam melakukan evaluasi state, didefinisikan suatu relasi : Untuk Q yang merupakan himpunan semua state
- D adalah himpunan state-state distinguishable, dimana D ⊂ Q
- N adalah himpunan state-state indistinguishable, dimana N ⊂ Q
- Maka, X ∈ N jika X ∈ Q dan X ∉ D
Contoh Sebuah Mesin DFA
Lakukan Reduksi State pada DFA diatas ?
Reduksi jumlah state pada FSA -Step
- State q5 tidak dapat dicapai dari state awal dengan jalan apapun (useless state). Hapus state q5.
- Catat state-state distinguishbale , yaitu :
q4 ∈ F sedang q0, q1, q2, q3 ∉ F sehingga pasangan-pasangan state :
- (q0,q1) = Distinguishable
- (q0,q2) = Distinguishable
- (q0,q3) = Distinguishable
- (q0,q4) = Distinguishable
- (q1,q2) = Belum terdefinisi
- (q1,q3) = Belum terdefinisi
- (q1,q4) = Distinguishable
- (q2,q3) = Belum terdefinisi
- (q2,q4) = Distinguishable
- (q3,q4) = Distinguishable
- Cari status pasangan lainnya dengan memperhatikan inputan yang tersedia yaitu 0 dan 1
- Pasangan (q0,q1)
- (q0,0) = q1 dan (q1,0) = q2 -> (q1,q2) belum terdefinisi
- (q0,1) = q3 dan (q1,1) = q4 -> (q3,q4) Distinguishable
- maka (q0,q1) adalah Distinguishable.
- Pasangan (q0,q2)
- (q0,0) = q1 dan (q2,0) = q1 -> (q1,q1) belum terdefinisi
- (q0,1) = q3 dan (q2,1) = q4 -> (q3,q4) Distinguishable
- maka (q0,q2) adalah Distinguishable.
- Pasangan (q0,q3)
- (q0,0) = q1 dan (q3,0) = q2 -> (q1,q2) belum terdefinisi
- (q0,1) = q3 dan (q3,1) = q4 -> (q3,q4) Distinguishable
- maka (q0,q3) adalah Distinguishable.
- Pasangan (q1,q2)
- (q1,0) = q2 dan (q2,0) = q1 -> (q2,q1) belum terdefinisi
- (q1,1) = q4 dan (q2,1) = q4 -> (q4,q4) belum terdefinisi
- maka (q1,q2) adalah belum terdefinisi
- Pasangan (q1,q3)
- (q1,0) = q2 dan (q3,0) = q2 -> (q2,q2) belum terdefinisi
- (q1,1) = q4 dan (q3,1) = q4 -> (q4,q4) belum terdefinisi
- maka (q1,q3) adalah belum terdefinisi
- Pasangan (q2,q3)
- (q2,0) = q1 dan (q3,0) = q2 -> (q1,q2) belum terdefinisi
- (q2,1) = q4 dan (q3,1) = q4 -> (q4,q4) belum terdefinisi
- maka (q2,q3) adalah belum terdefinisi
- Setelah semua pasangan state telah dipasangkan dengan setiap input yang ada maka terdapat state-state yang distinguishable yaitu :
- (q0,q1)
- (q0,q2)
- (q0,q3)
- (q0,q4)
- (q1,q4)
- (q2,q4)
- (q3,q4)
Karena berdasarkan relasi-relasi yang ada, tidak dapat dibuktikan (q1,q2), (q1,q3), dan (q2,q3) distinguishable, sehingga disimpulkan pasangan-pasangan state tersebut adalah Indistinguishable.
Reduksi Jumlah State pada FSA
Karena q1 indistinguishable dengan q2
q1 indistinguishable q3
q2 indistinguishable q3
makan dapat disimpulkan q1, q2, q3 saling indistinguishable dan dapat dijadikan satu state.
Berdasarkan hasil diatas, maka hasil DFA yang direduksi menjadi :
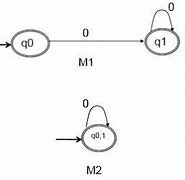
.png)
.png)



Comments
Post a Comment